Elliptic Curves, the fundamentals of ECDSA (Elliptic Curve Digital Signature Algorithm)

Overview

Elliptic curves play a pivotal role in modern cryptography, underpinning various protocols such as digital signatures, key exchange, and encryption. Elliptic Curve Cryptography (ECC) is a potent cryptographic method that leverages the mathematics of elliptic curves for public key encryption. As an alternative to the Rivest–Shamir–Adleman (RSA) cryptographic algorithm, which relies on prime factorization, ECC provides high security with smaller key sizes, making it a preferred choice in contemporary cryptographic systems.

ECC's main advantage is its efficiency. It offers high security with faster, shorter keys compared to RSA. This makes it ideal for mobile devices, which need to perform complex cryptographic operations with limited computational power. Furthermore, ECC is more resistant to attacks due to the difficulty of solving the elliptic curve discrete logarithm problem.

Elliptic curve

An elliptic curve is symmetric over the x-axis. This means that if a point (x, y) is on the curve, then the point (x, -y) is also on the curve. This property is a direct result of the equation used to define elliptic curves. If you replace y with -y in this equation, you'll see that the equation still holds, demonstrating the symmetry.

An elliptic curve is a smooth, plane curve defined by the equation:

\(y^2 = x^3 + ax + b\)

where

\(4a^3 + 27b^2 \neq 0\)

This equation represents the continuous form of an elliptic curve, which provides a visual and intuitive understanding of its properties. The curve is symmetric over the x-axis, meaning that for every point (x, y) on the curve, the point (x, -y) is also on the curve. This symmetry is a direct result of the equation defining the curve.

However, while this continuous representation is useful for understanding the elliptic curves, it's not the form we use in cryptography. In the world of cryptography, we work with a discrete version of elliptic curves. This means that instead of dealing with all real numbers, we only work with a finite set of numbers.

In the following sections, we will transition from this continuous representation to the discrete form of elliptic curves. This will allow us to delve into the fascinating applications of elliptic curves in the cryptographic landscape, where they play a crucial role in securing our digital communications. So, let's embark on this journey to explore the intriguing world of elliptic curves in cryptography.

The curve is defined over a finite field, which is usually represented by the symbol \(Z_q\), where q is a prime number.

The set \(Z_q\) of an elliptic curve is a finite field of prime order q. A finite field is a set of elements, where a set of operations (points addition, points subtraction, and point-scalar multiplication) are defined and obey certain mathematical properties. An elliptic curve is defined over a field \(Z_q\) and describes points in \(Z_q^2\) , the Cartesian product of \(Z_q\) with itself.

For example, in \(Z_{31}\) the field is made up of integers ranging from 0 to 30, and any operation within this field will yield an integer ranging from 0 to 30.

The curve is symmetric about the x-axis and has a single point at infinity, denoted by the letter O.

The point at infinity, denoted by O, is a unique point on an elliptic curve that serves as the identity element in the curve's group structure. It is a special point that is added to the curve to make the curve into a group. In other words, it is a point that serves as the zero of the curve.

The point at infinity can be thought of as the "missing point" that completes the curve. It is not a point in the usual sense, as it does not lie on the curve itself. Instead, it is a theoretical construct that allows for the definition of a group structure on the elliptic curve.

Elliptic curve - Wikipedia

Wikimedia Foundation, Inc.Contributors to Wikimedia projects

Elliptic curves on the plane can take various shapes depending on the values of a and b. Elliptic curves are symmetric about the x-axis, as can be easily seen and verified.

In order to achieve our goals, we will also require a point at infinity (also known as an identity element) to be a part of our curve. We will now use the symbol O or zero to represent our point at infinity.

If we want to explicitly include the point at infinity in our definition of an elliptic curve, we can do so as follows:

\( \{(x,y) \in Z_q^2 : y^2 \equiv x^3 + ax + b \mod{q}, 4a^3 + 27b^2 \neq 0 \} \cup \{0\} \)

Operations

The base operations of elliptic curve cryptography are point addition, point doubling, and scalar multiplication.

• Point Addition is the binary operation that is defined on the elliptic curve. It is used to add two points P and Q on the curve to produce a third point R. Point addition is defined as the reflection of point Q across the x-axis, followed by a line connecting the two points P and Q. The result is a new point R on the curve. The point at infinity, denoted by O, is the identity element of the group.

Properties:
• The identity element or O is the point at infinity.
• The point P's inverse is the one that is symmetric about the x-axis. For instance, if \(P = (P_x, P_y)\) then \(-P = (P_x, -P_y)\).
• If \(P + Q = R\) then \(R - Q = P\) and \(R - P = Q\)
• \(P - P = P + (-P) = 0\) • \((P + Q) + R = P + (Q + R)\)
• \(P + Q = Q + P\)

Algebraic formular: Given a curve \(E = \{(x,y) \in Z_q^2 : y^2 \equiv x^3 + ax + b \mod{q}, 4a^3 + 27b^2 \neq 0 \} \cup \{0\}\) and points on \(E\) , which are \(P\), \(Q\), and \(R = P + Q\), \(P = (P_x,P_y)\;,\;\; Q = (Q_x,Q_y)\;,\;\;R=(R_x,R_y)\).

\(m = \frac{Q_y - P_y}{Q_x - P_x} \mod q \\ R_x = m^2 - P_x - Q_x \mod q \\ R_y =m(P_x - R_x) - P_y \mod q \\\)

Python code:

def ecc_add(P, Q, q):
	m = ((Q[1] - P[1]) * pow(Q[0] - P[0],-1,q)) % q
	Rx = (m*m - P[0] - Q[0]) % q
	Ry = (m*(P[0] - Rx) - P[1]) % q
	return [Rx, Ry]

assert ecc_add([8,55], [385,277], 499) == [206, 428]

• Point doubling is the operation of adding a point P to itself on the curve. It is used to double the value of a point. For example, \(P + P = 2P, 2P + 2P = 4P, ...\) Algebraic formular: Given a curve \(E = \{(x,y) \in Z_q^2 : y^2 \equiv x^3 + ax + b \mod{q}, 4a^3 + 27b^2 \neq 0 \} \cup \{0\}\) and points \(P, Q = 2P\) on \(E\) where \(P = (P_x,P_y)\;,\;\; Q = (Q_x,Q_y)\). \(m = \frac{3P_x^2 + a}{2P_y} \mod q \\ Q_x = m^2 - 2P_x \mod q \\ Q_y =m(P_x - Q_x) - P_y \mod q \\\)

Python code:

def ecc_double(P, a, q):
	m = ((3*P[0]*P[0] + a) * pow(2*P[1],-1,q)) % q
	Qx = (m*m - 2*P[0]) % q
	Qy = (m*(P[0] - Qx) - P[1]) % q
	return [Qx, Qy]

assert ecc_double([8,55], 1, 499) == [385, 277]

• Scalar Multiplication is the operation of multiplying a point \(P\) on the curve by a scalar value k, resulting in a new point \(kP\). It is used in key generation and digital signatures, where a private key is a scalar value, and the corresponding public key is the result of scalar multiplication of the generator point \(G\) with the private key.

Properties:
• \(k_1P + k_2P = k_2P + k_1P = (k_1 + k_2)P\), For example \(2P = P + P, 3P = P + 2P, 4P = 3P + P, ...\)
• \((k_1)(k_2P)=(k_2)(k_1P)=(k_1k_2)P\) , For example \(2(3P) = 3(2P) = 6P\)

The generator point \(G\) of an elliptic curve is a point on the curve that generates all other points on the curve through repeated point addition. It is a specific point chosen on the curve that has a large order n, which is the number of times that point \(G\) can be added to itself to get back to the point at infinity O. The order n must be a prime number.

In cryptography, the generator point \(G\) is used as the base point for key generation and digital signatures. The private key is a scalar value k, and the corresponding public key is the result of the scalar multiplication of the generator point \(G\) with the private key, which is \(kG\). This means that the generator point $G$ can be used to generate a finite number of public keys for different private keys.

It's worth mentioning that the generator point \(G\) must be chosen carefully and it should be publicly known for the security of the system.

Python code:

def ecc_mul(point, scalar, a, q):
	if scalar == 0 or scalar >= q:
			raise Exception("Invalid Scalar/Private Key")
	scalar_bin = str(bin(scalar))[2:]
	tmp = point
	for i in range(1, len(scalar_bin)):
		tmp = ecc_double(tmp, a, q)
		if scalar_bin[i] == "1":
			tmp = ecc_add(tmp, point, q)
	return tmp

assert ecc_mul([8,55], 10, 1, 499) == [351, 155]

Extra note:

Finding the inverse of a scalar multiplication on an elliptic curve is a difficult problem and it is an important assumption used in modern cryptography today, as it is the basis for the security of various cryptographic protocols, and the security level is related to the size of the prime number p that defines the finite field over which the curve is defined, and the larger the p the more secure the system.

This problem is known as the Elliptic Curve Discrete Logarithm Problem (ECDLP).

The ECDLP is considered to be a difficult problem because it is a variant of the Discrete Logarithm Problem (DLP), which is a well-known hard problem in number theory. The DLP is the problem of finding an integer \(k\) such that \(a^k = b \mod p \;\) for a given \(a\), \(b\), and \(p\), where \(p\) is a prime number. The ECDLP is the same problem, but applied to the group of points on an elliptic curve.

The difficulty of solving the ECDLP is the basis for the security of various cryptographic protocols, such as digital signatures, key exchange, and encryption. In these protocols, the private key is a scalar value $k$, and the corresponding public key is the result of the scalar multiplication of the generator point \(G\) with the private key, which is \(kG\) . The security of the protocol relies on the assumption that it is difficult to find the private key \(k\) given the public key \(kG\) and the generator point \(G\) .

It's worth mentioning that there are several methods for solving the ECDLP, such as the Baby-Step Giant-Step, Pollard Rho, and index calculus, but they all have a high computational cost and the complexity of these methods increases as the size of the group increases, and the size of the group is related to the prime number $p$ that defines the finite field over which the curve is defined, so the larger the \(p\), the more secure the system.

Example of an elliptic curves

We'll set \(a=1, \; b=10, \; and \; q=499\) for the example curve (499 is a prime number), such that our curve will be \(E = \{(x,y) \in {\{0,1,2,...,498\}}^2 : y^2 \equiv x^3 + x + 10 \mod{499} \} \cup \{0\}\)

The curve displayed in the figure below is what we would typically get if we plotted the curve \(y^2 = x^3 + x + 10\) across an endless continuous field.

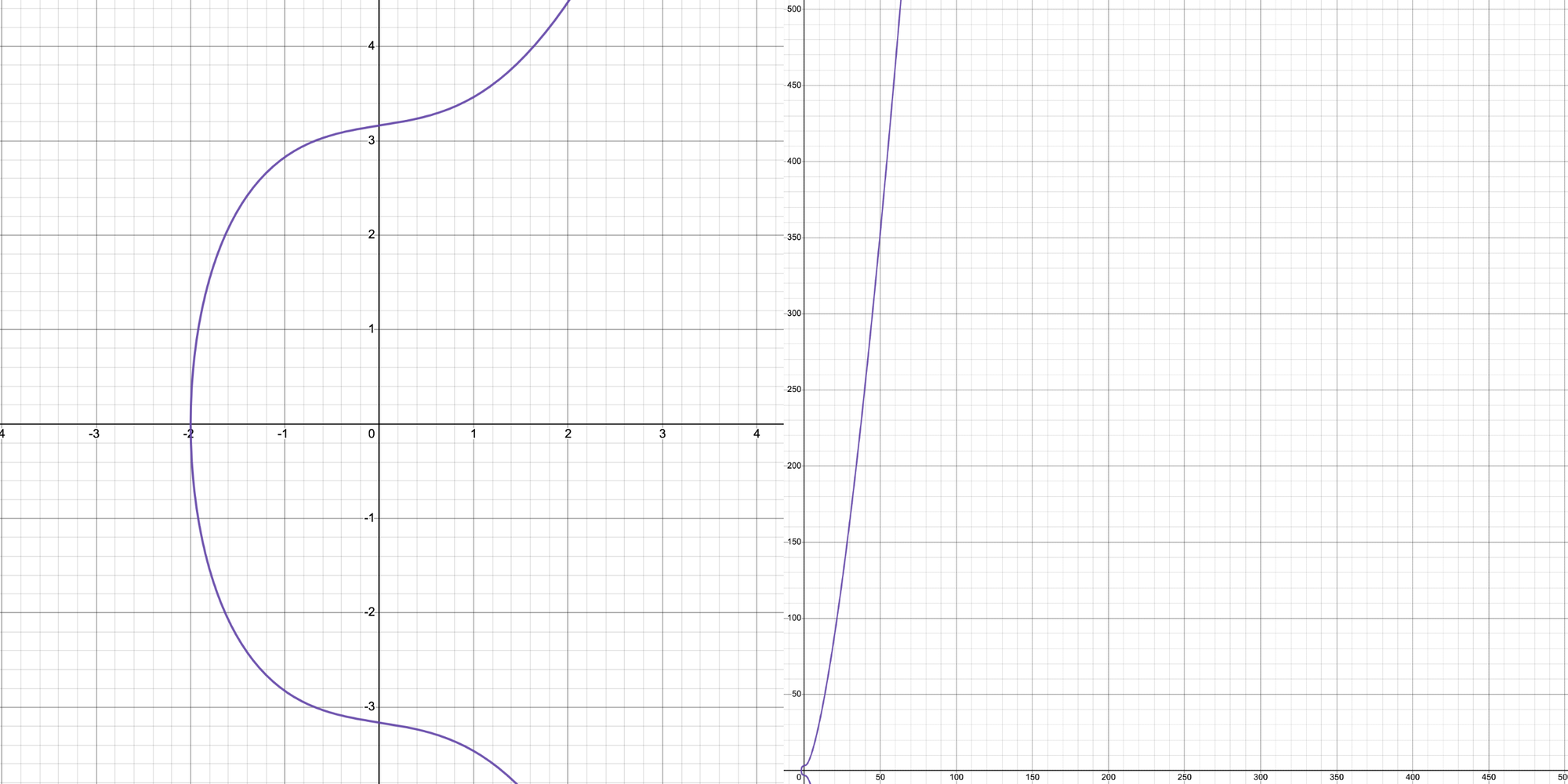
The collection of green dots in the figure below will appear instead if we plot E or a discrete form of \(y^2 = x^3 + x + 10\) in a finite field under a prime \(q = 499\). You can see that the purple continuous curve does not visibly coincide with the green continuous dots.

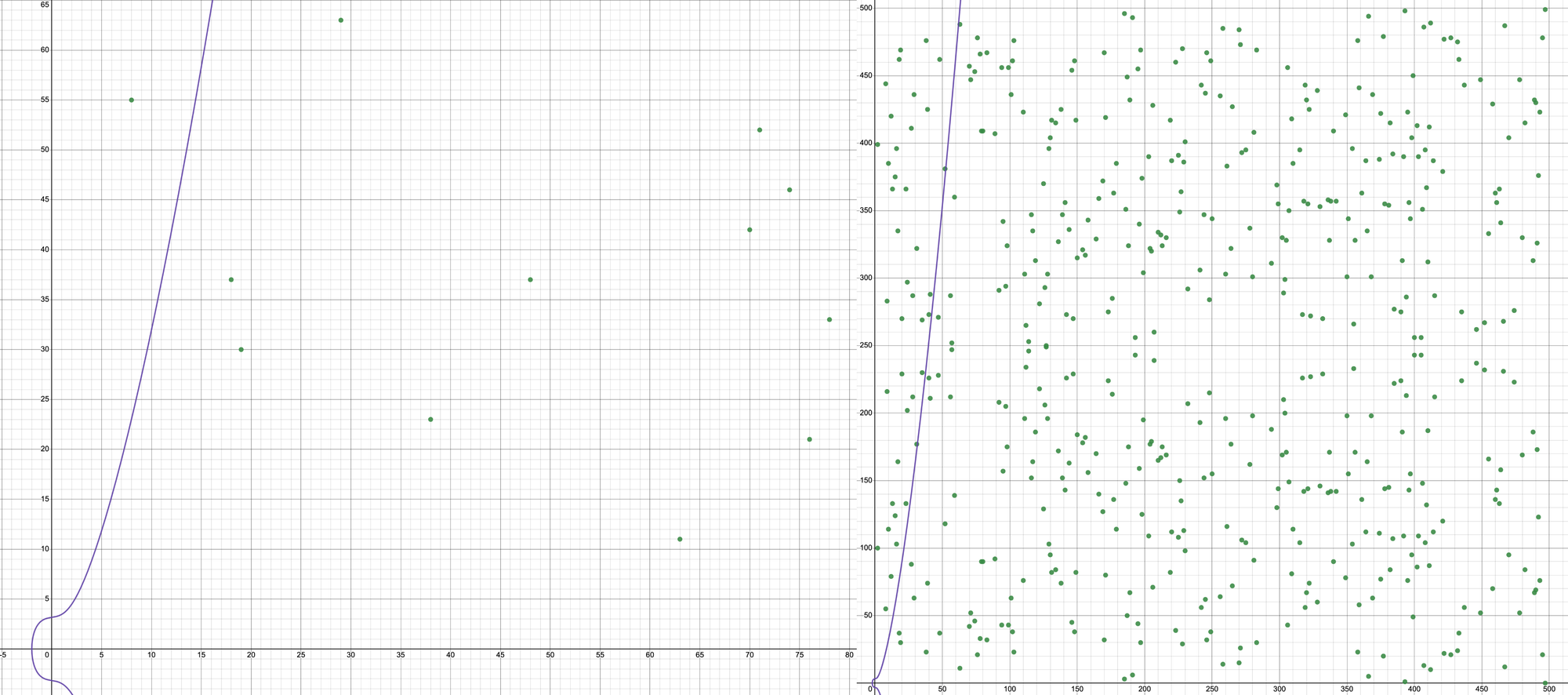
The set of green dots in the right figure represents all pairings of (x,y) positive integers that meet the condition that \(y^2 \mod{499} = (x^3 + x + 10)\mod{499}\), where x and y less than the prime number q = 499, for instance \((x,y) = (48,37)\).

The group of all points on an elliptic curve is so commonly referred to as an elliptic curve group or group (green dots). However, when working with elliptic curve cryptography, it is common to only work with a subset of the elliptic curve group or the subgroup rather than the entire group. This is because the security relies on the difficulty of solving the discrete logarithm problem. The subgroup is defined by \(G\), or the generator point, which may not span the entire group due to adding, doubling, and scalar multiplication, which usually makes the subgroup smaller than the group.

In the figure below, the green dots represent the group, while the black dots on the right represent the subgroup defined by \(G= (8,55)\).

The subgroup with \(G=(8,55)\) in the figure can be written explicitly as \(subgroup=\{G,2G,3G,...,nG\}\), where $n$ is the largest number that makes $nG$ unique for the subgroup. As a result, the element $n'G$ where $n' > n$ will be the repeated element that is already present in the subgroup.

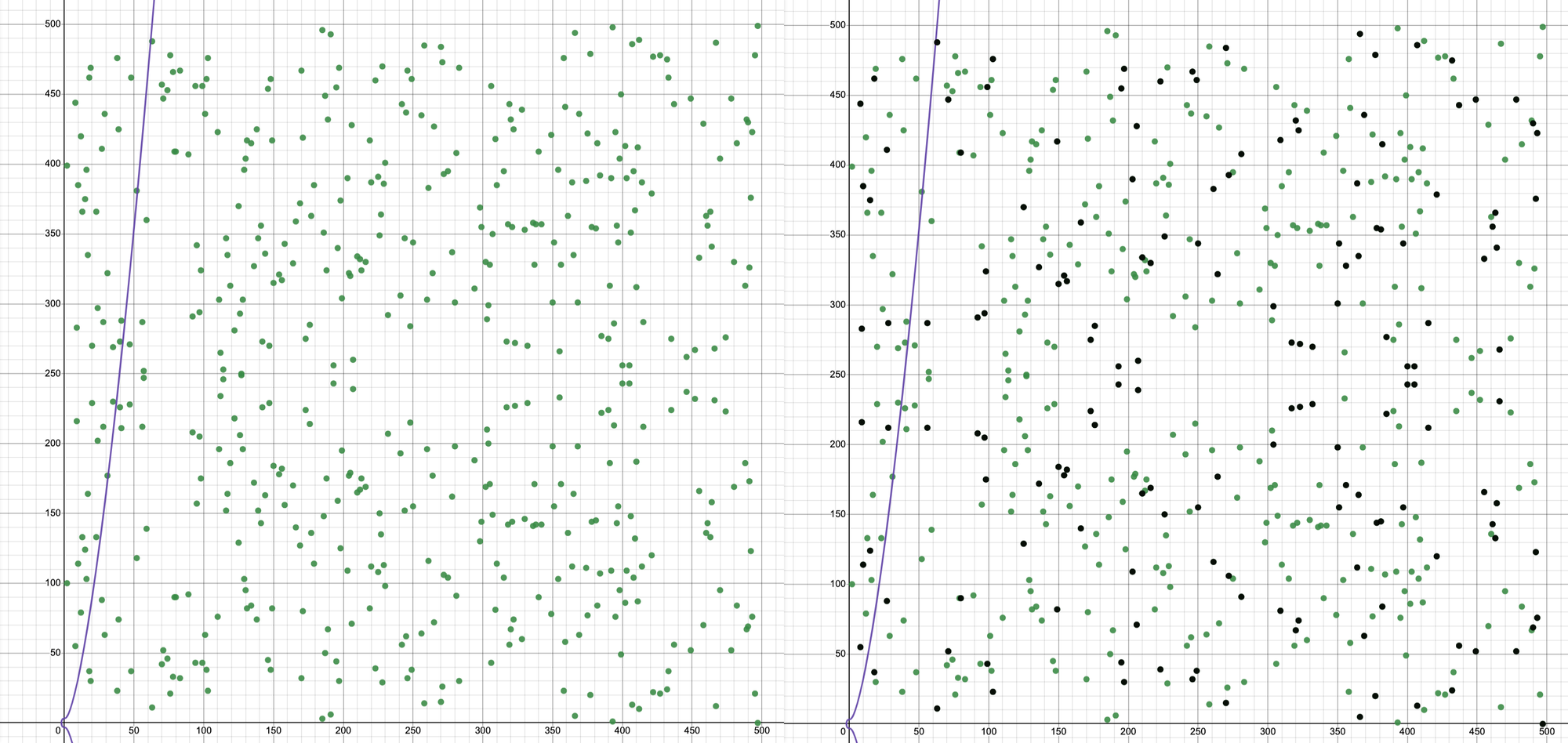
As you can see, all of the black dots overlap with the green dots, indicating that the subgroup is a subset of the group.

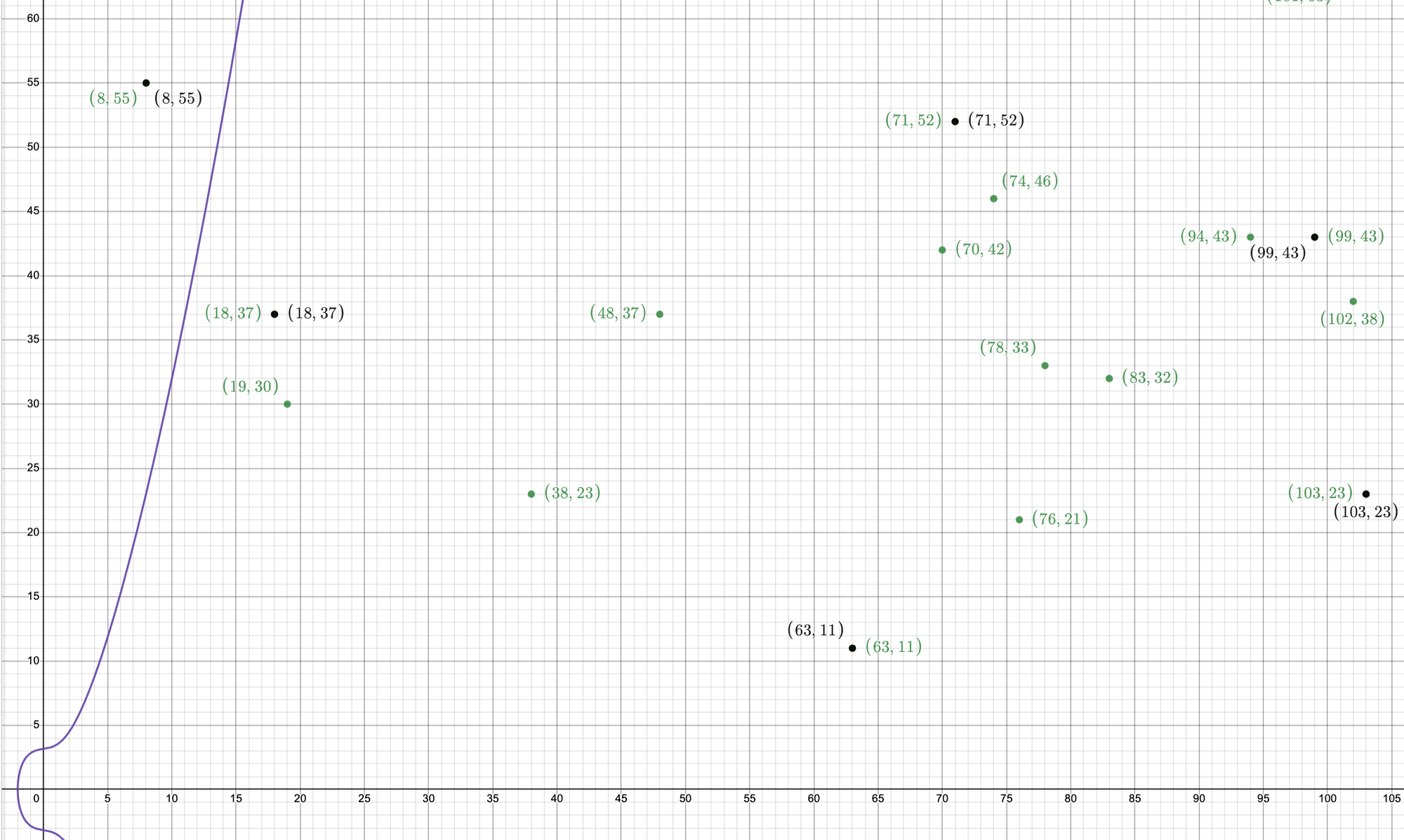
The black dots or subgroup also represent all possible public keys for the curve \(E = \{(x,y) \in {\{0,1,2,...,498\}}^2 : y^2 \equiv x^3 + x + 10 \mod{499} \} \cup \{0\} with  G= (8,55)\) as its generator.

Written By: Prin Rangsiruji, Band Protocol’s Senior Software Engineer